На составление первых появившихся в печати таблиц логарифмов их создатель Джон Непер потратил 20 лет. Джон Непер не был математиком. Он был любителем астрономии и математики.
Изобретение логарифмов в начале XVII в. тесно связано с развитием в XVI в. производства и торговли, астрономии и мореплавания, требовавших усовершенствования методов вычислительной математики. Всё чаще требовалось производить громоздкие действия над многозначными числами, всё большие требования предъявлялись к точности вычислений. Вот тогда-то и нашла воплощение идея логарифмов, ценность которых состоит в сведении сложных действий возведения в степень и извлечения корня к более простым действиям умножения и деления, а их в свою очередь к самым простым — сложению и вычитанию.
Происхождение этой идеи связано с сопоставлением двух числовых последовательностей следующего вида:
0, 1, 2, 3, 4, 5, … (1)
 (2)
(2)
Первая — последовательность неотрицательных целых чисел — представляет собой арифметическую прогрессию, вторая — геометрическую. Произведение любых двух членов последовательности (2) является членом этой же последовательности, который получается возведением числа в степень, равную сумме соответствующих членов последовательности (1). Эта идея была чётко выражена ещё в произведении Архимеда «Исчисление песчинок».
М. Штифель в «Полной арифметике» продолжает ряды (1) и (2) влево и впервые называет члены ряда (1) экспонентами, то есть показателями, членов ряда (2). При этом он пишет: «Сложение в арифметическом ряде соответствует умножению в геометрическом, равным образом вычитание в первом — делению во втором. Простому умножению в арифметическом ряде соответствует умножение на себя (возведение в степень) в геометрическом ряде, а деление в арифметическом ряде — извлечению корня в геометрическом ряде».
Таким образом, уже в середине XVI в. были разработаны основы учения о логарифмах. Не хватало только конкретных методов применения этой идеи в практических вычислениях, т. е. удобных логарифмических таблиц.
Логарифм и ощущения!
Человеческий организм способен испытывать различные ощущения. Интересно, что наш организм не только испытывает, но и «логарифмирует» эти ощущения.
Ощущения, воспринимаемые органами чувств человека, могут вызываться различными раздражениями, отличающимися друг от друга в миллиарды раз. Удары молота о стальную плиту в сто раз громче, чем шелест листьев, а яркость вольтовой дуги в миллионы раз превосходит яркость какой-нибудь слабой звезды на ночном небосклоне. Но никакие физиологические процессы не дают такого диапазона ощущений. Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, т. е. величина ощущений приблизительно пропорциональна десятичному логарифму величины раздражения.
Психофизический закон Фехнера гласит: величина ощущения пропорциональна логарифму величины раздражения.
Возьмём для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками...
Как видим, логарифмы вторгаются и в область психологии.
Логарифмическая спираль.
Логарифмическая спираль представляет собой кривую, которую описывает точка, движущаяся вдоль луча, равномерно вращающегося вокруг своего начала таким образом, что логарифм расстояния от точки до начала луча возрастает прямо пропорционально углу поворота луча. Обычно уравнение логарифмической спирали записывают, пользуясь в качестве основания системы логарифмов неперовым числом e. Такой логарифм числа r называют натуральным логарифмом и обозначают lnr. Итак, уравнение логарифмической спирали записывается в виде lnr = kα, где r — расстояние от точки до начала луча, α — угол поворота луча, k — коэффициент пропорциональности.
Эту кривую можно было бы назвать именем Декарта, поскольку впервые о ней говорится в одном из его писем. Однако подробное изучение её свойств было проведено только полвека спустя Якобом Бернулли. На его современников свойства произвели сильное впечатление. На каменной плите, водружённой на могиле этого знаменитого математика, изображены витки логарифмической спирали
.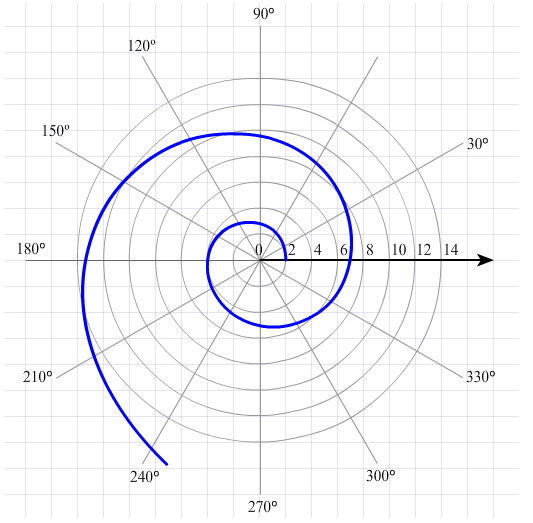
Из многих свойств логарифмической спирали отметим одно: любой луч, выходящий из начала, пересекает любой виток спирали под одним и тем же углом. Величина этого угла зависит только от числа k в уравнении спирали. При этом под углом между лучом и спиралью понимается угол между этим лучом и касательной к спирали, проведённой в точке пересечения.
Поразительно, что в природе логарифмические спирали встречаются на каждом шагу. По логарифмической спирали растут раковины разнообразных моллюсков, рога у многих животных. Во внутреннем ухе человека есть орган, называемый улитка, который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и также сотворена в форме логарифмической спирали. По спирали располагаются семена подсолнечника. По логарифмической спирали закручены и многие галактики, например галактика, которой принадлежит Солнечная система. И это далеко не все примеры.